B+树定义
一颗 m 阶的 B+树和 m 阶的 B-树的差异在于:
- 有 n 棵子树的结点中含有 n 个关键字;
在上一节中,在 B-树中的每个结点关键字个数 n 的取值范围为⌈m/2⌉ -1≤n≤m-1,而在 B+树中每个结点中关键字个数 n 的取值范围为:⌈m/2⌉≤n≤m。
- 所有的叶子结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
- 所有的非终端结点(非叶子结点)可以看成是索引部分,结点中仅含有其子树(根结点)中的最大(或最小)关键字。
例如,下图中所示的就是一棵深度为 4 的 3 阶 B+树:
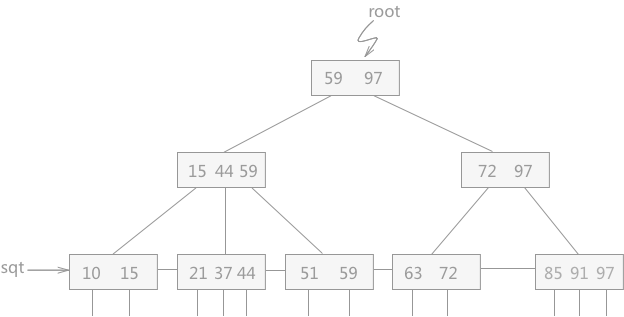
如上图所示,B+树中含有两个头指针,一个指向整棵树的根结点,另一个指向关键字最小的叶子结点。同时所有的叶子结点依据其关键字的大小自小而大顺序链接,所有的叶子结点构成了一个 sqt 指针为头指针的链表。
所有,B+树可以进行两种查找运算:一种是利用 sqt 链表做顺序查找,另一种是从树的根结点开始,进行类似于二分查找的查找方式。
在 B+树中,所有非终端结点都相当于是终端结点的索引,而所有的关键字都存放在终端结点中,所有在从根结点出发做查找操作时,如果非终端结点上的关键字恰好等于给定值,此时并不算查找完成,而是要继续向下直到叶子结点。
B+树的查找操作,无论查找成功与否,每次查找操作都是走了一条从根结点到叶子结点的路径。
B+树中插入关键字
在B+树中插入关键字时,需要注意以下几点:
- 插入的操作全部都在叶子结点上进行,且不能破坏关键字自小而大的顺序;
- 由于 B+树中各结点中存储的关键字的个数有明确的范围,做插入操作可能会出现结点中关键字个数超过阶数的情况,此时需要将该结点进行“分裂”;
B+树中做插入关键字的操作,有以下 3 种情况:
- 若被插入关键字所在的结点,其含有关键字数目小于阶数 M,则直接插入结束; 例如,在上图中插入关键字13,其结果如下图所示:
- 若被插入关键字所在的结点,其含有关键字数目等于阶数 M,则需要将该结点分裂为两个结点,一个结点包含⌊M/2⌋,另一个结点包含⌈M/2⌉。同时,将⌈M/2⌉的关键字上移至其双亲结点。假设其双亲结点中包含的关键字个数小于 M,则插入操作完成。 例如,在开始的图的基础上插入关键字 95,其插入后的 B+树如下图所示:
- 在第 2 情况中,如果上移操作导致其双亲结点中关键字个数大于 M,则应继续分裂其双亲结点。 例如,在开始的图的B+树中插入关键字 40,则插入后的 B+树如下图所示: 注意:如果插入的关键字比当前结点中的最大值还大,破坏了B+树中从根结点到当前结点的所有索引值,此时需要及时修正后,再做其他操作。例如,在图 1 的 B+树种插入关键字 100,由于其值比 97 还大,插入之后,从根结点到该结点经过的所有结点中的所有值都要由 97 改为 100。改完之后再做分裂操作。
B+树中删除关键字
在 B+树中删除关键字时,有以下几种情况:
- 找到存储有该关键字所在的结点时,由于该结点中关键字个数大于⌈M/2⌉,做删除操作不会破坏 B+树,则可以直接删除;
- 当删除某结点中最大或者最小的关键字,就会涉及到更改其双亲结点一直到根结点中所有索引值的更改;
- 当删除该关键字,导致当前结点中关键字个数小于⌈M/2⌉,若其兄弟结点中含有多余的关键字,可以从兄弟结点中借关键字完成删除操作;
- 第 3 种情况中,如果其兄弟结点没有多余的关键字,则需要同其兄弟结点进行合并;
- 当进行合并时,可能会产生因合并使其双亲结点破坏 B+树的结构,需要依照以上规律处理其双亲结点。
总之,在 B+树中做删除关键字的操作,采取如下的步骤:
- 删除该关键字,如果不破坏 B+树本身的性质,直接完成操作;
- 如果删除操作导致其该结点中最大(或最小)值改变,则应相应改动其父结点中的索引值;
- 在删除关键字后,如果导致其结点中关键字个数不足,有两种方法:一种是向兄弟结点去借,另外一种是同兄弟结点合并。(注意这两种方式有时需要更改其父结点中的索引值。)
本博文从 B+树 严长生 转载而来,表示感谢。
