B-树定义
B-树,有时又写为B_树(其中的“-”或者“-_只是连字符,并不读作“B减树”),一颗 m 阶的 B-树,或者本身是空树,否则必须满足以下特性:
- 树中每个结点至多有 m 棵子树;
- 若根结点不是叶子结点,则至少有两棵子树;
- 除根之外的所有非终端结点至少有棵子树;
- 所有的非终端结点中包含下列信息数据:(n,A0,K1,A1,K2,A2,…,Kn,An);
n 表示结点中包含的关键字的个数,取值范围是:⌈m/2⌉-1≤ n ≤m-1。Ki (i 从 1 到 n)为关键字,且 Ki < Ki+1 ;Ai 代表指向子树根结点的指针,且指针 Ai-1 所指的子树中所有结点的关键字都小于 Ki,An 所指子树中所有的结点的关键字都大于 Kn。
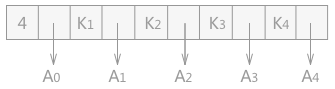
如图所示,当前结点中有 4 个关键字,之间的关系为:K1<K2<k3<K4。同时对于 A0 指针指向的子树中的所有关键字来说,其值都要比 K1 小;而 A1 指向的子树中的所有的关键字的值,都比 K1 大,但是都要比 K2 小。
- 所有的叶子结点都出现在同一层次,实际上这些结点都不存在,指向这些结点的指针都为 NULL;
例如图所示就是一棵 4 阶的 B-树,这棵树的深度为 4 :
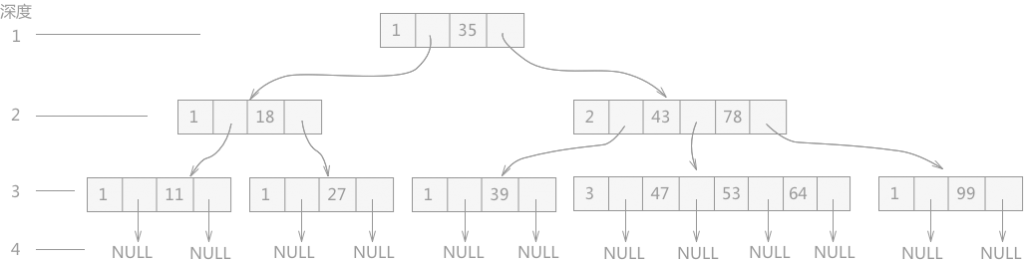
在使用 B-树进行查找操作时,例如在如上图所示的 B-树中查找关键字 47 的过程为:
- 从整棵树的根结点开始,由于根结点只有一个关键字 35,且 35 < 47 ,所以如果 47 存在于这棵树中,肯定位于 A1 指针指向的右子树中;
- 然后顺着指针找到存有关键字 43 和 78 的结点,由于 43 < 47 < 78,所以如果 47 存在,肯定位于 A1 所指的子树中;
- 然后找到存有 47、53 和 64 三个关键字的结点,最终找到 47 ,查找操作结束;
以上图中的 B-树为例,若查找到深度为 3 的结点还没结束,则会进入叶子结点,但是由于叶子结点本身不存储任何信息,全部为 NULL,所以查找失败。
B-树插入关键字
B-树也是从空树开始,通过不断地插入新的数据元素构建的。B-树在插入新的数据元素时并不是每次都向树中插入新的结点。
因为对于 m 阶的 B-树来说,在定义中规定所有的非终端结点(终端结点即叶子结点,其关键字个数为 0)中包含关键字的个数的范围是[⌈m/2⌉-1,m-1],所以在插入新的数据元素时,首先向最底层的某个非终端结点中添加,如果该结点中的关键字个数没有超过 m-1,则直接插入成功,否则还需要继续对该结点进行处理。
假设现在下图的基础上插入 4 个关键字 30、26、85 和 7:
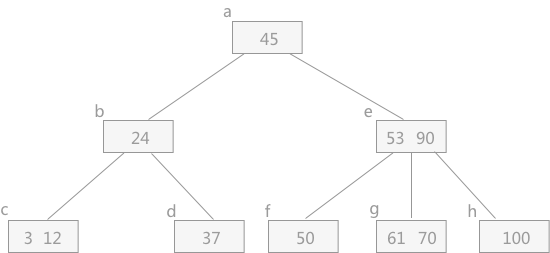
插入关键字 30 :从根结点开始,由于 30 < 45,所以要插入到以 b 结点为根结点的子树中,再由于 24 < 30,插入到以 d 结点为根结点的子树中,由于 d 结点中的关键字个数小于 m-1=2,所以可以将关键字 30 直接插入到 d 结点中。结果如下图所示:
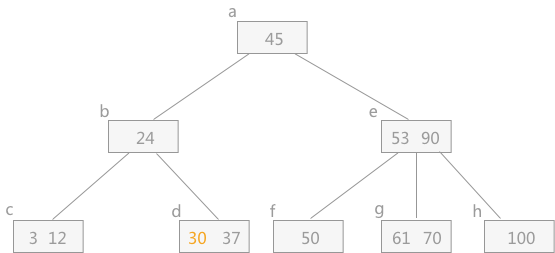
插入关键字 26:
从根结点开始,经过逐个比较,最终判定 26 还是插入到 d 结点中,但是由于 d 结点中关键字的个数超过了 2,所以需要做如下操作:
- 关键字 37 及其左右两个指针存储到新的结点中,假设为 d’ 结点;
- 关键字 30 存储到其双亲结点 b 中,同时设置关键字 30 右侧的指针指向 d’;
经过以上操作后,插入 26 后的B-树为:
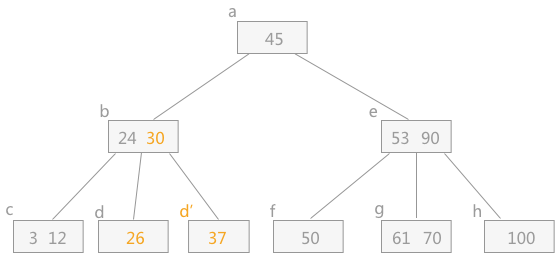
插入关键字 85:
从根结点开始,经过逐个比较,最终判定插入到 g 结点中,同样需要对 g 做分裂操作:
- 关键字 85 及其左右两个指针存储到新的结点中,假设为 g’ 结点;
- 关键字 70 存储到其双亲结点 e 中,同时设置 70 的右侧指针指向 g’ ;
经过以上操作后,插入 85 后的结果图为:
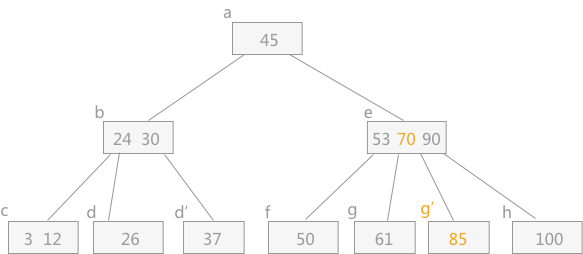
上图中,由于关键字 70 调整到其双亲结点中,使得其 e 结点中的关键字个数超过了 2,所以还需进一步调整:
- 将 90 及其左右指针存储到一个新的结点中,假设为 e’ 结点;
- 关键字 70 存储到其双亲结点 a 中,同时其右侧指针指向 e’ ;
最终插入关键字 85 后的 B-树为:
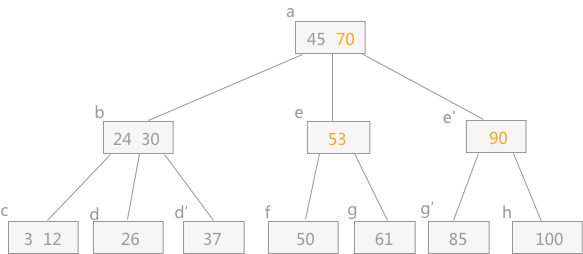
通过上边的例子,可以总结出一下结论:在构建 B-树的过程中,假设 p 结点中已经有 m-1 个关键字,当再插入一个关键字之后,此结点分裂为两个结点,如下图所示:
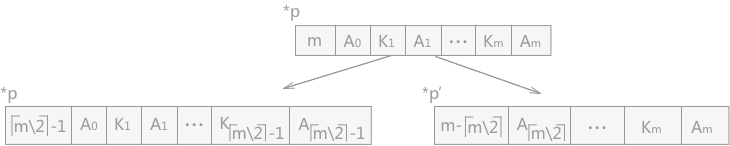
提示:如上图所示,结点分裂为两个结点的同时,还分裂出来一个关键字 K⌈m/2⌉,存储到其双亲结点中。
B-树删除关键字
在 B-树种删除关键字时,首先前提是找到该关键字所在结点,在做删除操作的时候分为两种情况,一种情况是删除结点为 B-树的非终端结点(不处在最后一层);另一种情况是删除结点为 B-树最后一层的非终端结点。
例如上边插入关键字的原始图来说,关键字 24、45、53、90属于不处在最后一层的非终端结点,关键字 3、12、37等同属于最后一层的非终端结点。
如果该结点为非终端结点且不处在最后一层,假设用 Ki 表示,则只需要找到指针 Ai 所指子树中最小的一个关键字代替 Ki,同时将该最小的关键字删除即可。
例如上边插入关键字的原始图中,如果要删除关键字 45 ,只需要使用关键字 50 代替 45 ,同时删除 f 结点中的 50 即可。
如果该结点为最后一层的非终端结点,有下列 3 种可能:
- 被删关键字所在结点中的关键字数目不小于⌈m/2⌉,则只需从该结点删除该关键字 Ki 以及相应的指针 Ai 。
- 例如,在上边插入关键字的原始图中,删除关键字 12 ,只需要删除该关键字 12以及右侧指向 NULL 指针即可。
- 被删关键字所在结点中的关键字数目等于⌈m/2⌉-1,而与该结点相邻的右兄弟结点(或者左兄弟)结点中的关键字数目大于⌈m/2⌉-1,只需将该兄弟结点中的最小(或者最大)的关键字上移到双亲结点中,然后将双亲结点中小于(或者大于)且紧靠该上移关键字的关键字移动到被删关键字所在的结点中。
例如在上边插入关键字的原始图中删除关键字 50,其右兄弟结点 g 中的关键字大于2,所以需要将结点 g 中最小的关键字 61 上移到其双亲结点 e 中(由此 e 中结点有:53,61,90),然后将小于 61 且紧靠 61 的关键字 53 下移到结点 f 中,最终删除后的 B-树如图所示。
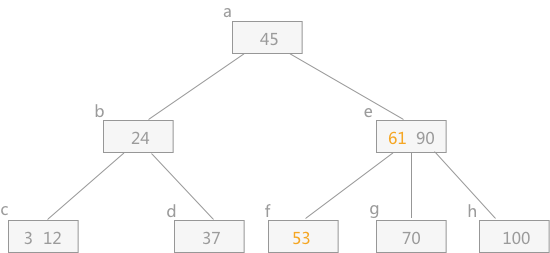
上图删除结点50后的B-树
- 被删除关键字所在的结点如果和其相邻的兄弟结点中的关键字数目都正好等于⌈m/2⌉-1,假设其有右兄弟结点,且其右兄弟结点是由双亲结点中的指针 Ai所指,则需要在删除该关键字的同时,将剩余的关键字和指针连同双亲结点中的 Ki 一起合并到右兄弟结点中。
例如,在上图中 B-树中删除关键字 53,由于其有右兄弟,且右兄弟结点中只有 1 个关键字。在删除关键字 53 后,结点 f 中只剩指向叶子结点的空指针,连同双亲结点中的 61(因为 61 右侧指针指向的兄弟结点 g)一同合并到结点 g 中,最终删除 53 后的 B-树为:
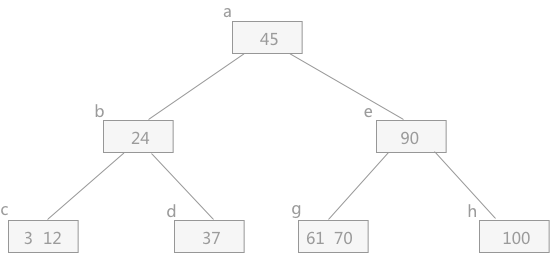
上图删除结点53后的B-树。
在合并的同时,由于从双亲结点中删除一个关键字,若导致双亲结点中关键字数目小于⌈m/2⌉-1,则继续按照该规律进行合并。例如在上图中 B-树的情况下删除关键字 12 时,结点 c 中只有一个关键字,然后做删除关键字 37 的操作。此时在删除关键字 37 的同时,结点 d 中的剩余信息(空指针)同双亲结点中的关键字 24 一同合并到结点 c 中,效果图为:
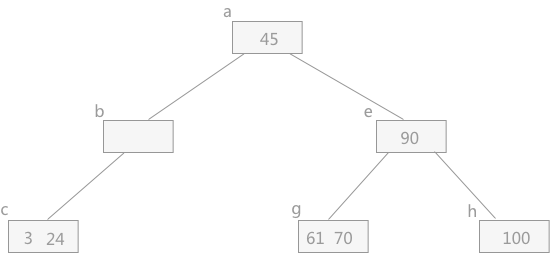
上图删除结点 37后的效果图。
由于结点 b 中一个关键字也没有,所以破坏了B-树的结构,继续整合。在删除结点 b 的同时,由于 b 中仅剩指向结点 c 的指针,所以连同其双亲结点中的 45 一同合并到其兄弟结点 e 中,最终的B-树为:
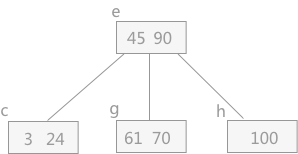
上图删除37后的B-树。
总结
由于 B-树具有分支多层数少的特点,使得它更多的是应用在数据库系统中。
本博文从 B-树 严长生 转载而来,表示感谢。
