Featured image of post 数据结构 静态树表查找算法
Algorithm

数据结构 静态树表查找算法

算法思想

在使用查找表中有n个关键字，表中的每个关键字被查找的概率都是1/n。在等概率的情况下，使用折半查找算法最优。

然而在某些情况下，查找表中的个关键字被查找的概率都是不同的。例如在UI设计师设计图片的时候，不同的设计师和不同的项目经理需求不同，有些项目经理喜欢暖色调，那么暖色调就会应用的多一些，有的项目经理比较喜欢冷色调，之后你的设计采用冷色调的概率也是比较大的。

在查找表中的关键字不同的情况下，对应于折半查找算法，按照上面的情况并不是最优的查找算法。

静态最优查找二叉树 若在考虑查找成功的情况下，描述查找过程的判定树其带权路径之和（用PH表示）最小时，查找性能最优。

算法思想例子

在查找表中各关键字查找概率不相同的情况下，对于使用折半查找算法，按照之前的方式进行，其查找的效率并不一定是最优的。例如，某查找表中有 5 个关键字，各关键字被查找到的概率分别为：0.1，0.2，0.1，0.4，0.2（全部关键字被查找概率和为 1 ），则根据之前介绍的折半查找算法，建立相应的判定树为（树中各关键字用概率表示）：

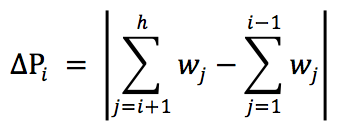
判定树公式

折半查找查找成功的平均查找长度计算方式：

ASL = 判定树中的各节点的查找概率 * 所在层次

相对的平均查找长度为：

ASL=0.41 + 0.22 + 0.22 + 0.13 + 0.1*3=1.8

带权路径之和的计算公式：PH = 所有结点所在的层次数 * 每个结点对应的概率值。

但是由于构造最优查找树花费的时间代价较高，而且有一种构造方式创建的判定树的查找性能同最优查找树仅差 1% – 2%，称这种极度接近于最优查找树的二叉树为次优查找树。

次优查找树的构建方法

构建二叉树方式

首先取出查找表中每个关键字及其对应的权值，采用如下公式计算出每个关键字对应的一个值：

构建二叉树

其中 wj 表示每个关键字的权值（被查找到的概率），h 表示关键字的个数。

表中有多少关键字，就会有多少个 △Pi ，取其中最小的做为次优查找树的根结点，然后将表中关键字从第 i 个关键字的位置分成两部分，分别作为该根结点的左子树和右子树。同理，左子树和右子树也这么处理，直到最后构成次优查找树完成。

算法实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

typedef int KeyType;//定义关键字类型
typedef struct{
    KeyType key;
}ElemType;//定义元素类型
typedef struct BiTNode{
    ElemType data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

//定义变量
int i;
int min;
int dw;
//创建次优查找树，R数组为查找表，sw数组为存储的各关键字的概率（权值），low和high表示的sw数组中的权值的范围
void SecondOptimal(BiTree T, ElemType R[], float sw[], int low, int high){
    //由有序表R[low...high]及其累计权值表sw（其中sw[0]==0）递归构造次优查找树
    i = low;
    min = abs(sw[high] - sw[low]);
    dw = sw[high] + sw[low - 1];
    //选择最小的△Pi值
    for (int j = low+1; j <=high; j++){
        if (abs(dw-sw[j]-sw[j-1])<min){
            i = j;
            min = abs(dw - sw[j] - sw[j - 1]);
        }
    }
   
    T = (BiTree)malloc(sizeof(BiTNode));
    T->data = R[i];//生成结点（第一次生成根）
    if (i == low) T->lchild = NULL;//左子树空
    else SecondOptimal(T->lchild, R, sw, low, i - 1);//构造左子树
    if (i == high) T->rchild = NULL;//右子树空
    else SecondOptimal(T->rchild, R, sw, i + 1, high);//构造右子树
   
}

时间复杂度

由于使用次优查找树和最优查找树的性能差距很小，构造次优查找树的算法的时间复杂度为 O(nlogn)，因此可以使用次优查找树表示概率不等的查找表对应的静态查找表（又称为静态树表）。

完整实例演示

例如，一含有 9 个关键字的查找表及其相应权值如下表所示：

查找表

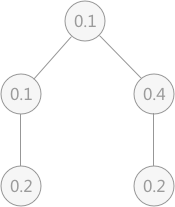
则构建次优查找树的过程如下：

首先求出查找表中所有的 △P 的值，找出整棵查找表的根结点：

查找根节点

例如，关键字 F 的 △P 的计算方式为：从 G 到 I 的权值和 – 从 A 到 E 的权值和 = 4+3+5-1-1-2-5-3 = 0。

通过上图左侧表格得知，根结点为 F，以 F 为分界线，左侧子表为 F 结点的左子树，右侧子表为 F 结点的右子树（如上图右侧所示），继续查找左右子树的根结点：

继续查找

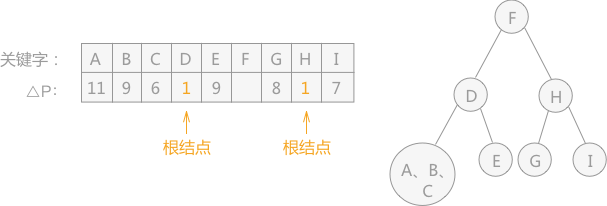
通过重新分别计算左右两查找子表的 △P 的值，得知左子树的根结点为 D，右子树的根结点为 H （如上图右侧所示），以两结点为分界线，继续判断两根结点的左右子树：

判定

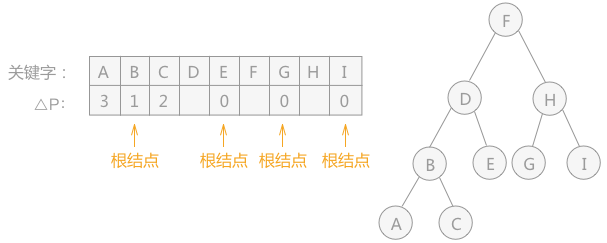
通过计算，构建的次优查找树如上图右侧二叉树所示。

后边还有一步，判断关键字 A 和 C 在树中的位置，最后一步两个关键字的权值为 0 ，分别作为结点 B 的左孩子和右孩子，这里不再用图表示。

注意：在建立次优查找树的过程中，由于只根据的各关键字的 P 的值进行构建，没有考虑单个关键字的相应权值的大小，有时会出现根结点的权值比孩子结点的权值还小，此时就需要适当调整两者的位置。

总结

在解决静态树表查找时，使用次优查找树的表示概率不等的查找表对应的静态查找表（又称静态树表）。

Reference